School of Mathematics & Statistics

Practical strategies for regression models for extremes

The generalised extreme value distribution (GEVD) plays a fundamental role in the theory of extreme values since it is the only possible limiting distribution of properly normalised maxima of a sequence of independent and identically distributed random variables. As such, it has been widely applied to approximate the distribution of maxima over blocks. In these applications, GEV properties such as finite lower endpoint when the shape parameter is positive or the loss of moments due to the magnitude of the shape parameter are inherited by the finite-sample maxima distribution. The extent to which these properties are realistic for the data at hand has been widely ignored. Motivated by these overlooked consequences in a regression setting, we here make three contributions:

1. We propose a blended GEV (bGEV) distribution that resembles the GEVD but with infinite support, thus avoiding any lower bound restrictions. Simulation studies reveal that the GEV and bGEV distributions are comparable when estimating the right tail under small and large sample settings.
2. We proposed a principled method called property-preserving penalised complexity (P³C) prior to deciding on the existence of the GEV distribution first and second moments a priori.
3. We propose a reparametrisation of the GEV distribution that provides a more natural interpretation of the (possibly covariate-dependent) model parameters, which in turn helps define meaningful priors.

The bGEV distribution with the new parameterisation and the P³C prior approach is implemented in the R-INLA package so it is readily available to users. This new distribution was used to model annual maxima of sub-daily precipitation, with the aim of producing spatial maps of return level estimates (Vandeskog et al., 2022). It was also used for extreme quantile regression using neural networks based on a new point process model, the so-called blended GEV point process model. Here, the GEVD is unsuitable since with neural networks, training crashes as soon as the algorithm jumps outside of the feasible parameter space, i.e., below the lower bound. This very practical issue is nicely solved by the bGEV distribution.

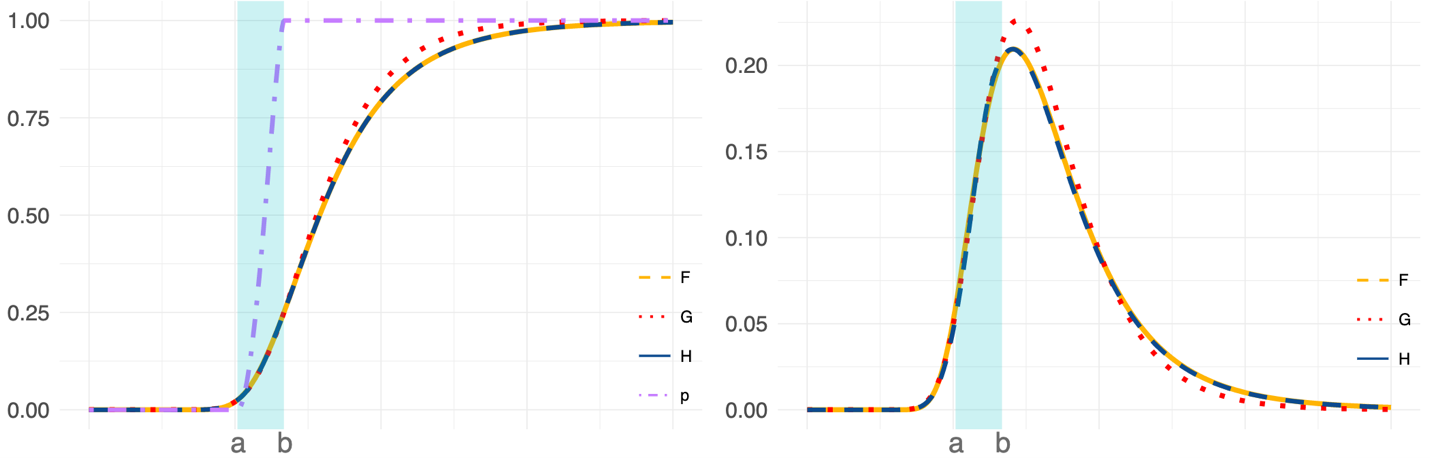
Illustration of the construction of the bGEV distribution (H) using Fréchet (F) and Gumbel (G) distributions. Distributions on the left and corresponding densities on the right. On the left, the purple dash-dotted line is the weight function p that combines F and G.