Modelling and Analysis of Material Systems
Real world physical systems are usually multiscale in nature. They are characterized by strong heterogeneities, geometrical complexity, and different constituents that interact across several hierarchical levels of organisation.
Typical examples include, but are not limited to, fluid flow through geometrically complex and porous structures (encountered, for instance, when dealing with oil and gas recovery problems or physiological fluid flow through biological tissues and organs [I]), and mechanical and chemical interactions among the various constituents of composite materials (such as, for example, soil or biological hard tissue, e.g. bone and tendons [II]).
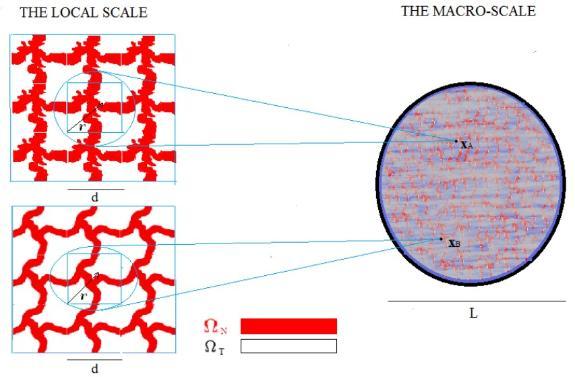
A schematic representing the microvascular heterogeneous tumour network (left) vs the macro (tissue) scale [I].
From a modelling viewpoint, it is necessary to have a comprehensive understanding of the qualitative and quantitative predictions (via analytical and numerical tools) for real-world phenomena to enable validation against appropriate experimental data.
This is basically a two-fold issue as (a) it is in general nontrivial and, especially for three-dimensional real problems, practically impossible to fully resolve microscale material and geometrical complexity and (b) experimental measurements usually provide average information on a macroscale, i.e. where the difference between different constituents cannot be easily detected.
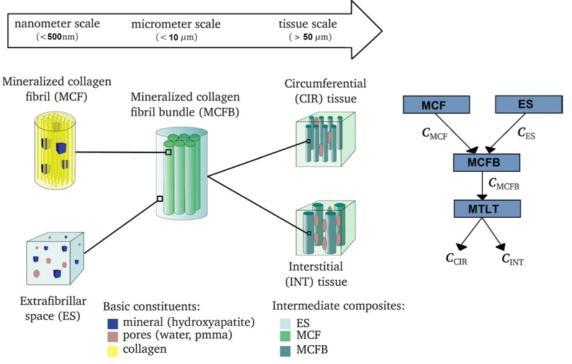
Multiscale structure of hierarchical hard tissue, e.g. bone and tendons [see also II, III]
These arguments have motivated the development of specific multiscale mathematical techniques designed to provide computationally feasible macroscopic mathematical models which encode the crucial role of the microstructure (in terms of material heterogeneities, geometry, fine scale physical coupling etc.).
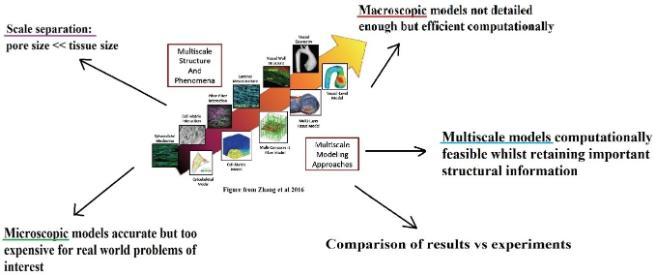
Different types of multiscale models bridge the phenomena found at different physiological scales in biological tissues e.g., arteries as in the above figure, see e.g. [IV] for an example concerning poroelastic composites.
At Glasgow, members of the Continuum Mechanics group use homogenisation techniques (such as asymptotic homogenisation, RVE-based and average field theories, perturbation methods), to describe the behaviour of real-world hierarchical materials via derivation and implementation of new system of partial differential equations (PDEs).
Current projects include investigations into: multiscale modelling of perfusion in avascular and vascular poroelastic tissues; multiscale modelling of healthy and aged/diseased bone and tendons; nematic liquid crystals flow in porous media chirality and flexoelectricity; improvement of current anti-cancer strategies, such as cancer hyperthermia and electrochemotherapy, via multiscale homogenisation of fluid and drug transport in vascularised tumours; development of a multiscale framework for mechanical and electrical activity in the heart.
References
[I] Penta, R., Ambrosi, D., & Quarteroni, A. (2015). Multiscale homogenization for fluid and drug transport in vascularized malignant tissues. Mathematical Models and Methods in Applied Sciences, 25(01), 79-108.
[II] Penta, R., et al. "Can a continuous mineral foam explain the stiffening of aged bone tissue? A micromechanical approach to mineral fusion in musculoskeletal tissues." Bioinspiration & biomimetics 11.3 (2016): 035004.
[III] Ramírez-Torres, Ariel, Raimondo Penta, Reinaldo Rodríguez-Ramos, José Merodio, Federico J. Sabina, Julián Bravo-Castillero, Raúl Guinovart-Díaz, Luigi Preziosi, and Alfio Grillo. "Three scales asymptotic homogenization and its application to layered hierarchical hard tissues." International Journal of Solids and Structures 130 (2018): 190-198.
[IV] Miller, Laura, and Raimondo Penta. "Effective balance equations for poroelastic composites." Continuum Mechanics and Thermodynamics 32.6 (2020): 1533-1557.

