Frobenius structures & geometric invariants
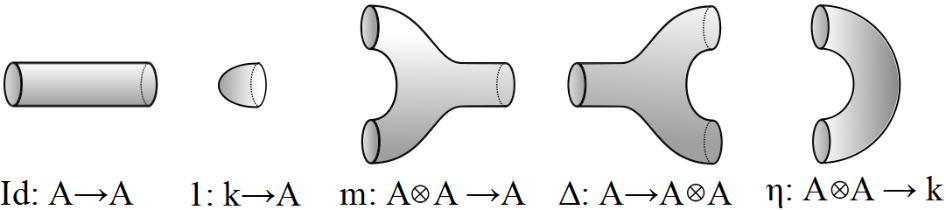
Figure: The structure maps of a Frobenius algebra (identity, unit, multiplication, co-multiplication and bilinear form) displayed as 2-cobordisms (left to right).
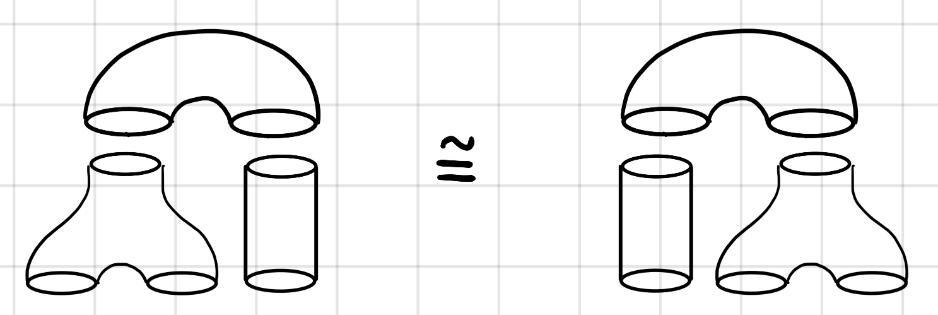
Figure: The 2-cobordism diagrams depicting the invariance of the bilinear form of a Frobenius algebra.
Background
Frobenius algebras are finite-dimensional, associative, unital algebras with an invariant non-degenerate bilinear form. They occur in many areas of mathematics, e.g. algebra and geometry, and are known to be categorically equivalent to two-dimensional topological quantum field theories. Prominent examples include the quantum cohomology or quantum K-theory rings of certain varieties, such as Grassmannians, or Verlinde algebras in conformal field theory, all of which are active areas of research in enumerative geometry and mathematical physics.
In the context of quantum integrable systems Frobenius algebras occur as solutions of the Bethe ansatz or quantum inverse scattering method. The latter is used when computing the partition function of a statistical lattice model or when diagonalising the Hamiltonians of a many-body system. Integrable systems can be used to compute the structure constants of these Frobenius algebras which in the mentioned examples are called Gromov-Witten invariants. There is also a link to soliton theory via Witten’s conjecture (proved by Kontsevich) linking solutions (tau-functions) of the Korteweg-de Vries hierarchy to these geometric invariants.
More generally, families of Frobenius algebras give rise to the notion of a Frobenius manifold introduced by Dubrovin in the 1990s. Any Frobenius manifold is equipped, in particular, with a flat metric and a multiplication in every tangent space which form a Frobenius algebra. Frobenius manifolds have rich differential geometry. In addition to quantum cohomology, integrable hierarchies and topological field theories, Frobenius manifold structures arise also on orbit spaces of reflection groups and in singularity theory.
Researchers
Publications
- Trigonometric V-systems and solutions of WDVV equations, Journal of Physics A: Mathematical and Theoretical, 54, (2021).
- V-Systems, Holonomy Lie Algebras, and Logarithmic Vector Fields, International Mathematics Research Notices, 2018(7), (2018).
- Yang–Baxter algebras, convolution algebras, and Grassmannians, Russian Mathematical Surveys, 75(5), (2020).
- Quantum integrability and generalised quantum Schubert calculus, Advances in Mathematics, 313, (2017).
- From quantum Bäcklund transforms to topological quantum field theory, Journal of Physics A: Mathematical and Theoretical, 49, (2016).
Grants

