Many-Body Systems
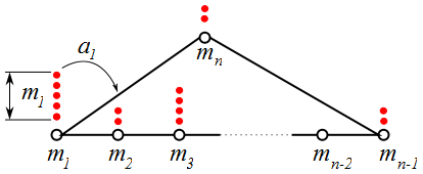
Figure: The Verlinde algebra (a Frobenius algebra) of the Wess-Zumino-Witten conformal field theory for su(n) can be described as a quantum many-body system of impenetrable bosons with hard-core interaction on a circular lattice on n-sites.
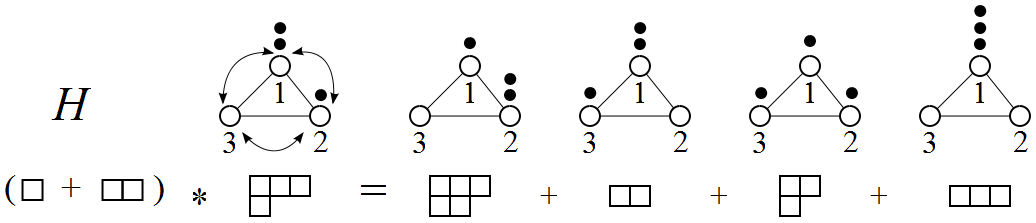
Figure: The Hamiltonian of the system is described as multiplication operator within the Verlinde algebra involving the hopping of bosons to neighbouring sites.
Background
It remains a tantalising challenge to find exact solutions for many-body systems in classical as well as quantum mechanics. Integrable systems are an important class of systems where this is possible due to the high number of integrals of motion, the latter usually arise from rich underlying algebraic and geometric structures.
Important examples are given by Calogero-Moser, Macdonald-Ruijsenaars-Schneider and Toda systems due to their deep relations to geometry and algebra. These integrable systems are intimately related to (double) affine Hecke and Cherednik algebras and their representations, multivariable orthogonal polynomials, their phase spaces provide interesting Poisson varieties.
Certain discrete quantum many-body systems, such as a quantum spin-chains, are linked to lattice models in statistical mechanics: the lattice row configurations of the lattice model are interpreted as a snapshot in time of a quantum many-body system and the statistical transfer matrix is viewed in this context as a discrete time evolution operator. For example, the ice or six-vertex model is linked to the Heisenberg spin-chain which describes ferromagnetic materials. This mathematical connection between statistical lattice models and quantum many-body systems means that they both share the same underlying algebraic structures used in their solutions: quantum groups, Hecke and Temperley-Lieb algebras.
Another example to arrive at solvable quantum many-body systems is via quantisation of classical integrable systems with soliton solutions. Roughly speaking, the solitons become quantum particles and exact expressions for their two-particle scattering amplitudes can be computed, for instance in the case of affine Today field theories, by using Coxeter geometry.
Researchers
Publications
- Generalized Calogero–Moser systems from rational Cherednik algebras, Selecta Mathematica New Series, 18, (2012).
- Generalized Macdonald–Ruijsenaars systems, Advances in Mathematics, 250, (2014).
- Intertwining operator for AG2 Calogero–Moser–Sutherland system, Journal of Mathematical Physics, 60(7), (2019).
- Quasi–invariant Hermite Polynomials and Lassalle–Nekrasov Correspondence, Communications in Mathematical Physics, 386, (2021).
- The sl(n)k-WZNW fusion ring: A combinatorial construction and a realisation as quotient of quantum cohomology, Advances in Mathematics, 225(1), (2010).
- PT symmetry on the lattice: the quantum group invariant XXZ spin chain, Journal of Physics A: Mathematical and Theoretical, 40(30), (2007).
- On the universal representation of the scattering matrix of affine Toda field theory, Nuclear Physics B, 567(3), (2000).
Grants

