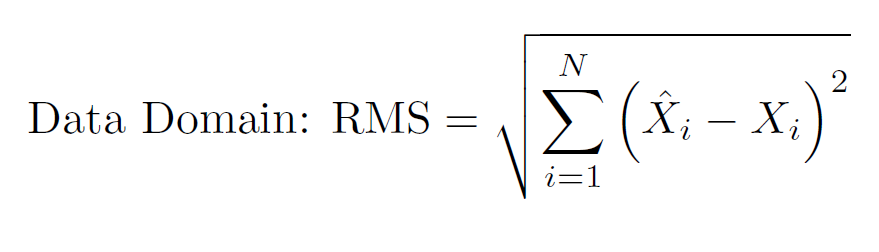Assessment Criteria for Cside 2018

 

Different iterations of Cside may explore different criteria as to rank the performance of the participating methods. This will allow us to gain a deeper understanding of our methods and perhaps address specific questions of interest e.g. convergence capabilities or classification of outcomes.

This year's criteria will be estimation accuracy of the data generating parameters. Accuracy will be assessed both in the parameter domain and the data domain. There will be three criteria:

• Parameter Domain: Weighted Root Mean Square (RMS). Competitors will submit a point estimate for each parameter in their chosen model. From these estimates, the data generating parameters will be subtracted. The differences will be weighted by the data generating parameters to avoid different parameter magnitudes from dominating the calculation. The RMS will then be calculated.

         In the above calculation, p is the number of parameters in the model, θ_i(hat) is the i^th parameter point estimate of the competitor and θ_i is the i^th parameter that generated the data. Methods that produce smaller RMS values are ranked better.

 

• Data Domain: Root Mean Square (RMS). Competitors will use their point estimate for each parameter in their chosen model and solve the system of equations. This produces a predicted signal. From these predicted signals, the signal produced with the data generating parameters will be subtracted. The RMS will then be calculated.

 

‌In the above calculation, N is the total number of data points, X_i(hat) is the i^th data point produced by solving the system with the competitor's estimates and X_i is the i^th data point using the parameters that generated the data. Methods that produce smaller RMS values are ranked better.‌ Please note that Model 3 will not be assessed by this criterion, since Model 3 is a Stochastic Differential Equation.

 

• Parameter Domain: Likelihood. This criterion is included in order to assess a method's uncertainty quantification. Competitors will submit a point estimate for each parameter in their chosen model and either a standard deviation/standard error corresponding to each parameter or a precision matrix corresponding to all parameters. The likelihood (assuming a Gaussian distribution) of the data generating parameters given the competitor's estimates and standard deviations/standard errors/precision matrix will then be calculated.

 

‌‌In the above calculation, p is the number of parameters in the model, N(...) denotes the Gaussian distribution, θ_i(hat) is the i^th parameter point estimate of the competitor, θ_i is the i^th parameter that generated the data, σ_i is the i^th standard deviation/standard error corresponding to the i^th parameter estimate, θ(hat) is the vector of parameter point estimates of the competitor, θ is the vector of parameters that generated the data and Σ is the precision matrix corresponding to all parameter estimates. Methods that produce larger likelihood values are ranked better.

 

Overall Scoring

Competitors will receive a rank for each of the above criterion based on how well their method scored relative to the rest of the competitors for their chosen model (methods will not be compared between models). A competitor's overall score will be the average rank across criteria.