Dr Robert Teed
- Senior Lecturer (Mathematics)
telephone:
0141 330 5674
email:
Robert.Teed@glasgow.ac.uk
Room 424, School of Mathematics & Statistics, University of Glasgow, University Place, Glasgow, G12 8QQ
https://orcid.org/0000-0003-2831-3116Biography
Visit my personal website for more details.
-
Aug 2023 - date: Senior Lecturer in Applied Mathematics
-
Sept 2017 - Aug 2023: Lecturer in Applied Mathematics
School of Mathematics and Statistics, University of Glasgow
-
Oct 2014 - Aug 2017: Research Associate
-
Sept 2011 - Sept 2014: Research Associate
-
Oct 2007 - July 2011: PhD in Applied Mathematics
School of Mathematics, University of Leeds (Thesis title: The effects of zonal flow on rapidly rotating convection in planetary interiors)
-
Oct 2002 - June 2006: MMath in Mathematics & Physics
Research interests
| Magnetohydrodynamics |  |
|
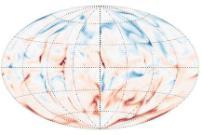
Planetary dynamos including the geodynamo |
 |
|
The solar dynamo and solar cycle |
 |
|
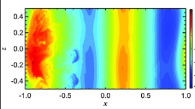
Convection in astrophysical and geophysical bodies |
 |
Research summary:
My research involves the theoretical/numerical modelling of fluid systems in the presence of rotation, magnetic fields, and shear flows. To do this I use various numerical techniques (and computer power) to solve the equations relevant to fluid dynamics and magnetic field generation. My research has applications to Earth's core, the Sun's atmosphere, planetary atomspheres, protoplanetary discs, and other astrophysical objects.
This research is primarily motivated by a desire to better understand the fluid dynamics - including convection processes - and magnetic field generation - the 'dynamo process' - within planets and stars. In particular, numerical simulations are able to provide insight into the dynamics of the chaotic fluid regions (e.g. Earth's liquid iron outer core, the solar convection zone, planetary atomspheres) where magnetic fields are generated.
If you are a prospective PhD student and would like to know more about possible projects in my research area, then please look at the 'Supervision' section below.
Research groups
Grants
STFC Standard Grant (PI), "The force hierarchy in planetary dynamo models", 2024-2027, (ST/Y00146X/1)
Supervision
I am currently interested in taking on more PhD students. If you are a prospective PhD student and would like to know more about the projects below, then please get in touch with me: Robert.Teed@glasgow.ac.uk.
Potential PhD projects:
- Modelling the force balance in planetary dynamos.
Current simulations of magnetic field (the 'dynamo process') generation in planets are run, not under the conditions of planetary cores and atmospheres, but in a regime idealised for computations. To forecast changes in planetary magnetic fields such as reversals and dynamo collapse, it is vital to understand the actual fluid dynamics of these regions. The aim of this project is to produce simulations of planetary cores and atmospheres with realistic force balances and, in doing so, understand how such force balances arise and affect the dynamics of the flow. The importance of different forces (e.g. Coriolis, Lorentz, viscous forces) determine the dynamics, the dynamo regime, and hence the morphology and strength of the magnetic field that is produced. This project would involve working with existing numerical code to perform the simulations and developing new techniques to determine the heirarchy of forces at play.
 |  |  |
|---|
- Identifying waves in dynamo models.
This project would involve using existing (and developing new) techniques to isolate and study MHD waves in numerical calculations. Various classes of waves exist and may play a role in the dynamo process and/or help us better understand changes in the magnetic field.
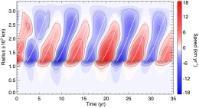
- The effects of magnetic fields on zonal flows in planetary interiors.
This project would involve analytical and numerical solutions of equations governing (magneto)convection in simplified geometries. For example, the Jovian atmosphere can be modelled using plane or annular geometries which simplfy the solutions to the governing equations. The aim would be to better understand how a magnetic field can affect the jets of Jupiter's atmosphere.
- Modelling the solar dynamo and solar cycle.
This project would use simulations to look at the roles shear flow and helicity could play in generating the Sun's magnetic field and producing the 11-year solar cycle.
Current PhD students:
- Hunter, Emma
Numerical simulations of planetary and stellar dynamos - Sarwar, Ayesha
The zoo of stellar and planetary dynamos - Stanish, Sage Alek
Topological constraints in magnetohydrodynamics
Teaching
Current teaching:
Mathematics 2A: Multivariable Caluclus (Moodle page) (2022-)
Previous teaching:
Mathematics 1 (2019-2022)
3H/S Mathematical Methods (2017-2019)
5M Applied Mathematical Methods (SMSTC) (2017-2019)
Tutor for courses (past and present):
- Mathematics 1, Mathematics 1X, Mathematics 1Y;
- Mathematics 2A, Mathematics 2B;
- 3H/3S Mathematical Methods, 3H/3Q: Mechanics of Rigid and Deformable Bodies, 3H/3U Methods in Complex Analysis, 3H/3V Dynamical Systems;
- 4H/5E Partial Differential Equations;
- 5M Applied Mathematical Methods (SMSTC).
