School of Mathematics & Statistics

Birational Geometry

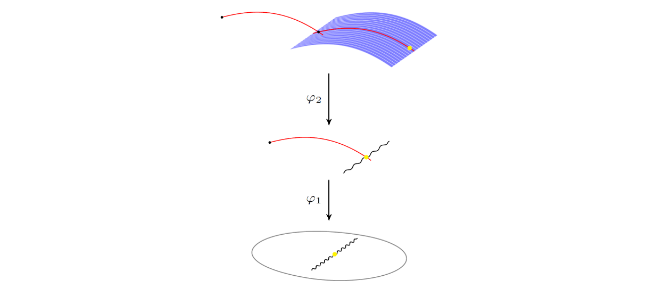
Birational geometry is the study of algebraic varieties up to birational equivalences. Loosely speaking, this flexibility allows us to perform surgeries which manipulate the variety into a more pleasant form.  Many of the motivating questions for the group in Glasgow are in low dimension, where techniques from noncommutative algebra are being used to classify the most elementary surgery of 3-dimensional flops, to realise crepant resolutions via geometric invariant theory (GIT), and to approach questions around whether curves are contractible.  There are various global consequences, and links to other geometric topics such as curve-counting invariants.