Quantitative recurrence and hyperbolicity for the Teichmüller flow.
Ian Frankel (Toronto)
Monday 1st April, 2019 16:00-17:00
Maths 311B
Abstract
We will explain how quantitatively recurrent geodesics for the Teichmüller metric on the moduli space of Riemann surfaces behave like geodesics in a negatively curved space. More precisely,
Let :%090%09%5Cleq%09t%09%5Cleq%09L%5C%7D) be the family of quadratic differentials corresponding to a length
be the family of quadratic differentials corresponding to a length  segment of a Teichmüller geodesic, parametrized by the metric. Let
segment of a Teichmüller geodesic, parametrized by the metric. Let 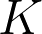 be a compact subset of the moduli space of Riemann surfaces. If the set of times
be a compact subset of the moduli space of Riemann surfaces. If the set of times  for which
for which 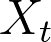 belongs to
belongs to 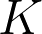 has measure at least
has measure at least  , and contains
, and contains  and
and  , we will explain why the unit neighborhood of
, we will explain why the unit neighborhood of ) in its strongly stable leaf is contracted by
in its strongly stable leaf is contracted by  in some metric, where the constants
in some metric, where the constants  depend on
depend on 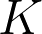 and
and 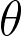 but not
but not  .
.
Add to your calendar
Download event information as iCalendar file (only this event)

