Full factors and coamenable inclusions
Jon Bannon (Siena College)
Thursday 23rd May, 2019 16:00-17:00
Maths 311B
Abstract
If a factor is full then every approximately inner automorphism is inner. We have the following generalization: If a factor  is full, then the any correspondence of
is full, then the any correspondence of  weakly equivalent to the trivial correspondence must contain the trivial correspondence. This generalization provides a perspective that allows us to prove that if
weakly equivalent to the trivial correspondence must contain the trivial correspondence. This generalization provides a perspective that allows us to prove that if  is a coamenable inclusion with faithful, normal conditional expectation and
is a coamenable inclusion with faithful, normal conditional expectation and  a full factor, then there is a nonzero
a full factor, then there is a nonzero  so that
so that 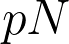 is full. As a corollary, this affirmatively answers Problem 3.3.2 of Popa's correspondences preprint from 1986. Furthermore, we use this to prove that if a compact group
is full. As a corollary, this affirmatively answers Problem 3.3.2 of Popa's correspondences preprint from 1986. Furthermore, we use this to prove that if a compact group  acts on a full factor
acts on a full factor  then the action is minimal, i.e.
then the action is minimal, i.e. '%5Ccap%09M=%5Cmathbb%7BC%7D1) . Consequently, for any such action by results of Izumi, Longo and Popa there is a Galois correspondence between the intermediate subalgebras of
. Consequently, for any such action by results of Izumi, Longo and Popa there is a Galois correspondence between the intermediate subalgebras of  and fixed point subalgebras of the closed subgroups of
and fixed point subalgebras of the closed subgroups of  .
.
Add to your calendar
Download event information as iCalendar file (only this event)

