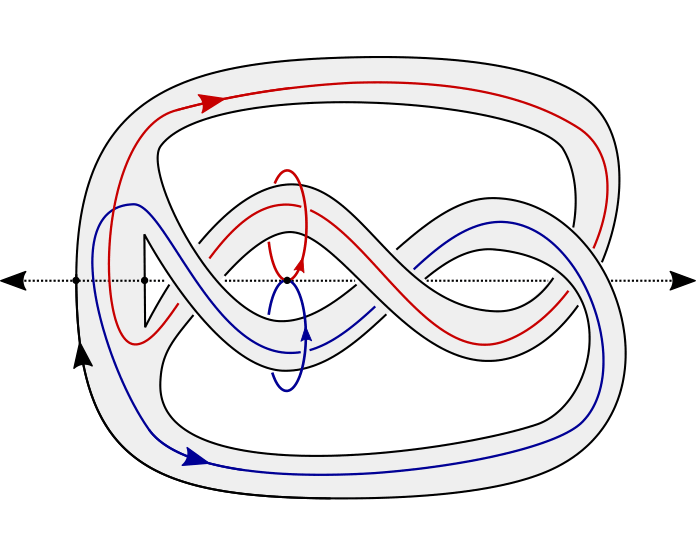
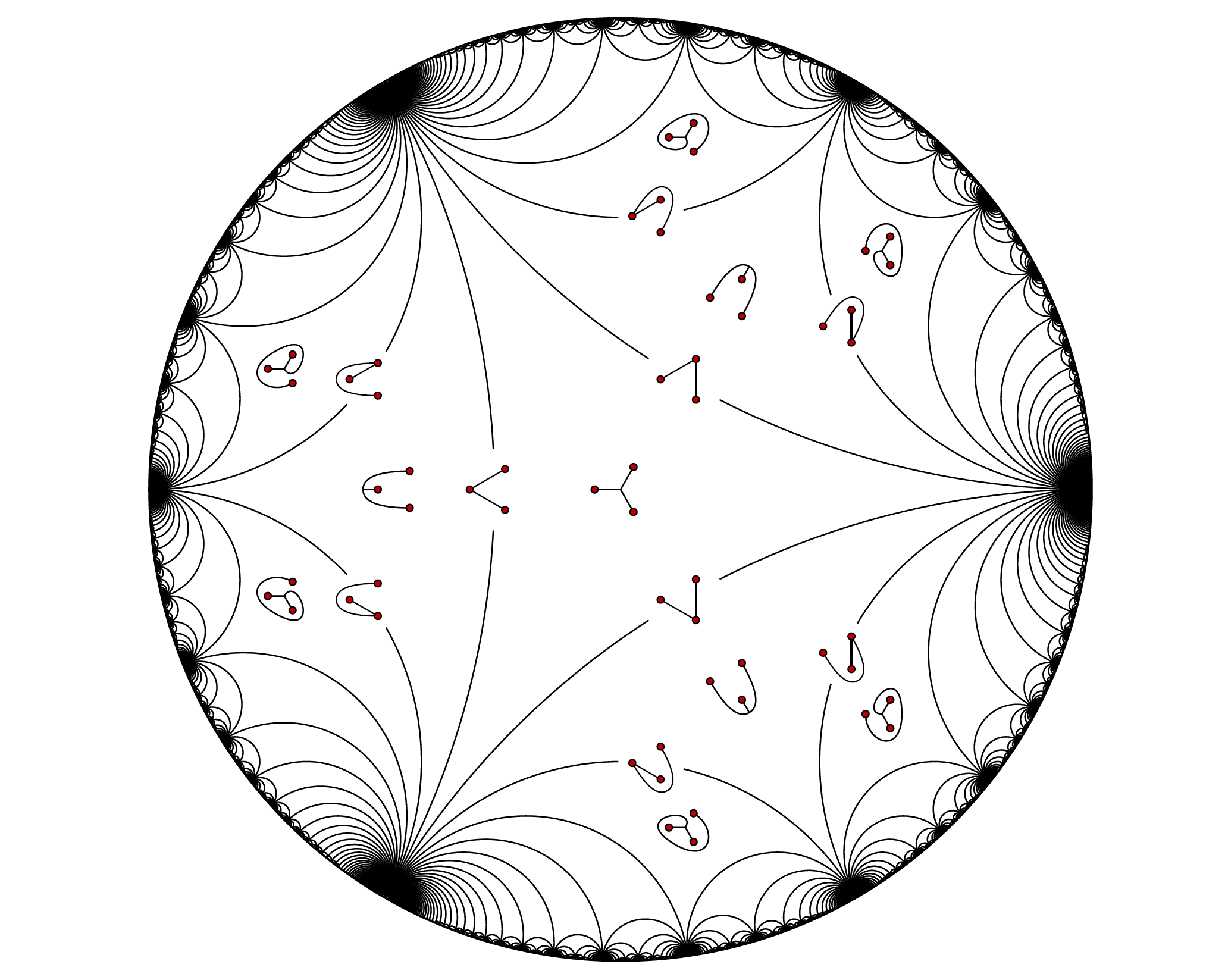
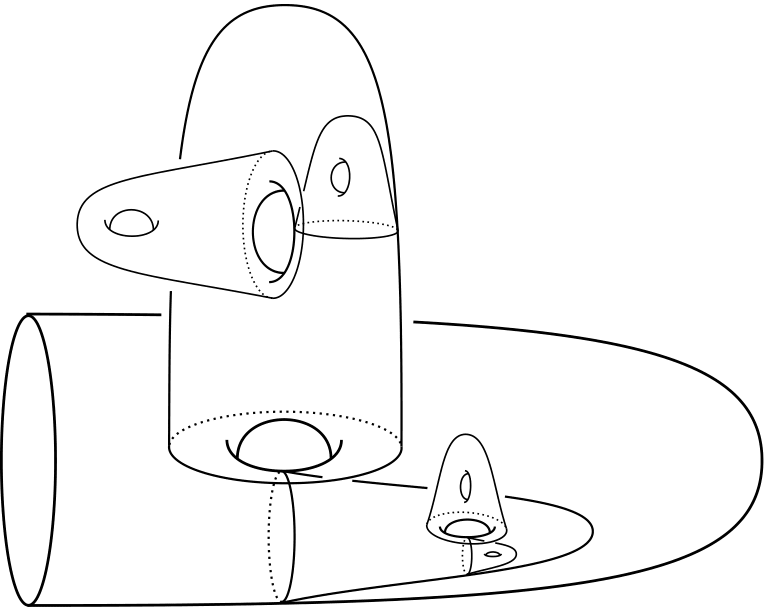
The study of such objects brings together ring theory, topology and algebraic geometry and has applications in integrable systems and mathematical physics.
Geometry and Topology
-
A deformation of a singularity
-
A braid
Braids appear spontaneously in both topology and category theory, for reasons that turn out to reveal deep connections between these subjects.
Research activity in Geometry and Topology occurs in several areas, including that of Category Theory.
Our interests in Geometry cover a broad range of topics including: algebraic geometry; differential geometry; geometric group theory; and interactions with differential equations, representation theory and string theory.
Our interests in Topology encompass low-dimensional topology and algebraic topology. While the study of these subjects often involves geometric intuition, Topologists tend to study much less `rigid' geometric situations than Geometers.
Category theory looks at mathematics on a large scale. The aim is to strip away inessential details in order to get to the essence of things.
Dr Chris Athorne Senior lecturer
Geometric representation theory; algebraic curves;soliton theory
Member of other research groups: Integrable Systems and Mathematical Physics
Research student: Sophie Rachel Norman
Dr Andrew J Baker Reader
Hopf algebras and formal groups; stable homotopy theory;structured ring spectra and derived algebraic geometry; Morava K-theory for classifying spaces of finite groups and fusion systems
Member of other research groups: Algebra
Dr Gwyn Bellamy Lecturer
D-module, symplectic algebraic geometry, deformation-quantization algebras
Member of other research groups: Algebra
Dr Tara Brendle Lecturer
Geometric group theory; mapping class groups of surfaces; low-dimensional topology
Member of other research groups: Algebra
Research students: Neil Fullarton, Charalampos Stylianakis, Alan Logan
Prof Kenneth A Brown Professor of Mathematics
Noncommutative algebra; Hopf algebras; homological algebra
Member of other research groups: Algebra
Research students: Astrid Jahn, Paul Gilmartin
Dr Mikhail Feigin Lecturer
Quantum integrable systems; Hadamard's problem; WDVV equations; random matrices; Representations of Chrednik algebras; rings of quasi-invariants
Member of other research groups: Integrable Systems and Mathematical Physics, Algebra
Dr James Griffin Research Associate
Operads; Loop spaces; (Co)homology theories of algebras
Member of other research groups: Algebra
Supervisor: Ulrich Kraehmer
Dr Brendan Owens Lecturer
Low-dimensional topology: knots, 3-manifolds, smooth 4-manifolds
Research students: Andrew Donald, Duncan Mc Coy
Dr Richard J Steiner Senior lecturer
Category theory
Dr Daniel Stevenson Lecturer
Abstract homotopy theory; category theory; gerbes
Research student: Pouya Adrom
Prof Ian A B Strachan Professor of Mathematical Physics
Geometry and integrable systems; Frobenius manifolds; twistor theory and self-duality
Member of other research groups: Integrable Systems and Mathematical Physics
Research student: Richard Stedman
Dr Christian Voigt Lecturer
Noncommutative geometry; K-theory; Quantum groups
Dr Raymond Vozzo Lecturer
Differential geometry; gerbes; infinite-dimensional geometry.
Dr Stuart White Senior Lecturer
Non-commutative geometry
Member of other research groups: Algebra, Analysis
Research students: Liam Dickson, Tomasz Pierzchala, Jorge Castillejos Lopez
Dr Andrew Wilson University Teacher of Mathematics
Dr Joachim Zacharias Reader
C*-algebras, their classification and amenability properties; special examples of C*-algebras; K-theory and non commutative topology, noncommutative dynamical systems, geometric group theory with applications to C*-algebras.
Member of other research groups: Integrable Systems and Mathematical Physics, Analysis, Algebra
Research students: Andrew Hawkins, Gabriel Tornetta
Pouya Adrom PhD Student
Research Topic: Topics in abstract homotopy theory
Supervisor: Daniel Stevenson
Barry Devlin PhD Student
Research Topic: Category Theory
Member of other research groups: Algebra
Andrew Donald PhD Student
Research Topic: Seifert manifolds which embed in the four-sphere
Supervisor: Brendan Owens
Neil Fullarton PhD Student
Research Topic: Mapping class groups and related groups
Member of other research groups: Algebra
Supervisor: Tara Brendle
Astrid Jahn PhD Student
Research Topic: Hopf algebras
Member of other research groups: Algebra
Supervisor: Kenneth A Brown
Duncan Mc Coy PhD Student
Research Topic: Knots and Smooth Four-Dimensional Manifolds
Supervisor: Brendan Owens
Ana Rovi PhD Student
Research Topic: Lie algebroids
Member of other research groups: Algebra
Supervisor: Ulrich Kraehmer
Charalampos Stylianakis PhD Student
Research Topic: Mapping Class Groups and Related Groups
Member of other research groups: Algebra
Supervisor: Tara Brendle
Friday 10th May14:00-15:00Mathematics 417
Prof. F. Quinn (Virginia Polytechnic Institute and State Universit)
Monday 13th May16:00-17:00Mathematics 325
Dr C. Wendl (University College London)
Monday 20th May14:30-15:30tba
A. J. Harju (University of Helsinki )
Monday 20th May16:00-17:00Mathematics 325
Dr A. Wilson (University of Glasgow)
Monday 3rd June16:00-17:00Mathematics 325
Dr J. Giansiracusa (Swansea University)